Kelompok Besaran di Bawah Ini Yang Merupakan Kelompok Besaran Turunan Adalah …
As an expert in the field, I’ll delve into the topic of kelompok besaran di bawah ini yang merupakan kelompok besaran turunan adalah … to provide a comprehensive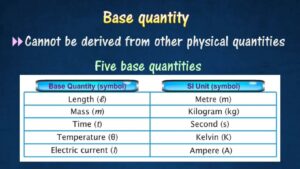 
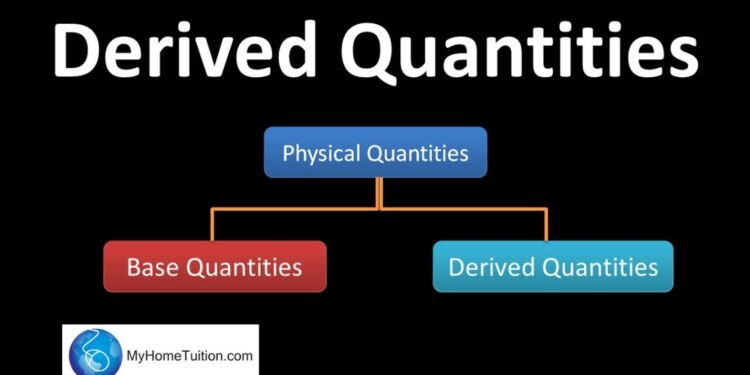
understanding. When it comes to identifying groups of derived quantities, it’s crucial to grasp the fundamental concepts that underpin these classifications.
One key aspect to consider is the relationship between base and derived quantities. By discerning how derived quantities are derived from base units through mathematical combinations, we can pinpoint which groups fall under the category of derived quantities. This connection forms the cornerstone of categorizing various physical parameters within distinct frameworks.
In exploring this subject further, we’ll unravel the intricate web of units and measurements, kelompok besaran di bawah ini yang merupakan kelompok besaran turunan adalah … shedding light on how different types of quantities align with one another. Understanding these relationships not only enhances our knowledge but also paves the way for a deeper comprehension of the interconnected nature of physical measurements.
Understanding Derived Quantities
In the realm of physics and mathematics, derived quantities play a crucial role in extending our understanding of the physical world kelompok besaran di bawah ini yang merupakan kelompok besaran turunan adalah …. These quantities are derived from fundamental base quantities through mathematical operations or formulas. They provide us with deeper insights into various phenomena and help quantify complex relationships between different physical parameters.
Characteristics of Derived Quantities:
- Derived quantities are not independent but rely on base quantities for their definition.
- They often have units that are combinations of base units, showcasing how they are interconnected.
- Understanding derived quantities requires a solid grasp of the underlying principles and equations governing their derivation.
Examples in Everyday Life:
- Velocity: A classic example of a derived quantity is velocity, which is defined as the rate of change of displacement with respect to time. It combines the base quantities of length (meters) and time (seconds).
- Acceleration: Another vital derived quantity is acceleration, representing the rate at which an object’s velocity changes over time. It involves the base quantities of length and time squared.
- Force: Force, expressed in newtons, arises from mass multiplied by acceleration—a fundamental equation in physics illustrating how derived quantities emerge from basic principles.
Significance in Scientific Research:
Derived quantities serve as building blocks for scientific research across various disciplines. From calculating sophisticated astronomical trajectories to analyzing intricate chemical reactions, these quantities underpin much of what we know about the physical universe. Scientists rely on them to formulate hypotheses, conduct experiments, and draw meaningful conclusions that advance our collective knowledge.
By delving into the intricacies of derived quantities, we uncover a rich tapestry woven from fundamental principles and mathematical relationships. Each calculation involving these entities unveils layers of complexity while simplifying our comprehension of natural processes. Embracing the elegance inherent in derived quantities propels us towards greater discoveries and a more profound appreciation for the beauty of scientific inquiry.
Definition of Derived Quantities
Exploring the realm of physics, we encounter a fascinating concept known as derived quantities. These are measurements that stem from fundamental base quantities through mathematical operations like multiplication, division, or exponentiation. In simpler terms, derived quantities are derived from combining base quantities in various ways.
When we delve into the world of physics and its intricate calculations, derived quantities play a pivotal role. They help us understand complex relationships between different 
physical phenomena by providing us with measurable units for specific combined parameters. For example, velocity is a derived quantity obtained by dividing displacement by time.
In essence, derived quantities serve as building blocks in constructing the language of physics. They allow us to express intricate concepts and relationships in succinct numerical terms. As we manipulate these derived quantities through equations and formulas, we unravel the mysteries of the physical universe around us.
By grasping the significance of derived quantities, we gain a deeper appreciation for how interconnected various physical properties are. From acceleration to force to energy, each derived quantity tells a unique story about the underlying principles governing our world. Embracing these interwoven measurements enhances our understanding of nature’s laws and enriches our exploration of the cosmos.
